给定n个矩阵{A 1 ,A 2 ,…,A n },其中Ai与A i+1 是可乘的,i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
例如:
A 1 ={30x35} ; A 2 ={35x15} ;A 3 ={15x5} ;A 4 ={5x10} ;A 5 ={10x20} ;A 6 ={20x25} ;
结果为:((A 1 (A 2 A 3 ))((A 4 A 5 )A 6 )) 最小的乘次为15125。
原问题为n个矩阵连乘,将原问题分解为子问题,即当n等于1,2,3…..时。
n==1 时,单一矩阵,不需要计算。最小乘次为0
n==2 时,根据n==1时的结果,遍历计算出每相邻两个矩阵的最小乘次
n==3 时, 根据n==1和n==2时的结果 ,此时已经求出 每相邻1个、2个矩阵的最小乘次 ,遍历计算出该相邻三个矩阵的最小乘次
依次类推……
当 n==n 时, 根据n==1、2、……n-1时的结果 ,此时已经求出 每相邻1个、2个、3个……n-1个矩阵的最小乘次 ,由此求出n==n时的最小乘次
每当n增加1时,就利用已求出的子结构来求解此时的最优值。
数学描述如下:
设矩阵Ai的维数为 P i × P i+1 。
设 A[i:j] 为矩阵A i A i+1 ….A j 的连乘积,即从Ai到Aj的连乘积,其中,0 <= i <= j <= n-1
设m [i][j] 为计算A[i:j]的最小乘次,所以 原问题的最优值为m[0][n-1] 。
当 i==j 时,单一矩阵,无需计算。 m[i][i]=0 ,i=0,1,….n-1
当 i < j 时,利用最优子结构,计算m[i][j]。即寻找断开位置k (i <= k < j) ,使得 m[i][k]+m[k+1][j]+P i P k+1 P j+1 最小。
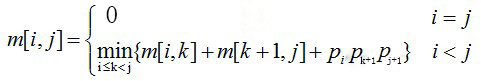
该算法的python实现:
# coding=gbk
# 矩阵连乘问题
__author__ = 'ice'
# row_num 每个矩阵的行数
class Matrix:
def __init__(self, row_num=0, col_num=0, matrix=None):
if matrix != None:
self.row_num = len(matrix)
self.col_num = len(matrix[0])
else:
self.row_num = row_num
self.col_num = col_num
self.matrix = matrix
def matrix_chain(matrixs):
matrix_num = len(matrixs)
count = [[0 for j in range(matrix_num)] for i in range(matrix_num)]
flag = [[0 for j in range(matrix_num)] for i in range(matrix_num)]
for interval in range(1, matrix_num + 1):
for i in range(matrix_num - interval):
j = i + interval
count[i][j] = count[i][i] + count[i + 1][j] + matrixs[i].row_num * matrixs[i + 1].row_num * matrixs[j].col_num
flag[i][j] = i
for k in range(i + 1, j):
temp = count[i][k] + count[k + 1][j] + matrixs[i].row_num * matrixs[k + 1].row_num * matrixs[j].col_num
if temp < count[i][j]:
count[i][j] = temp
flag[i][j] = k
traceback(0, matrix_num - 1, flag)
return count[0][matrix_num - 1]
def traceback(i, j, flag):
if i == j:
return
if j - i > 1:
print(str(i + 1) + '~' + str(j + 1), end=': ')
print(str(i + 1) + ":" + str(flag[i][j] + 1), end=',')
print(str(flag[i][j] + 2) + ":" + str(j + 1))
traceback(i, flag[i][j], flag)
traceback(flag[i][j] + 1, j, flag)
matrixs = [Matrix(30, 35), Matrix(35, 15), Matrix(15, 5), Matrix(5, 10), Matrix(10, 20), Matrix(20, 25)]
result = matrix_chain(matrixs)
print(result)
# 1~6: 1:3,4:6
# 1~3: 1:1,2:3
# 4~6: 4:5,6:6
# 15125

